本节主要介绍了VLSI DSP中的流水线与并行处理技术，以提高处理效率或降低功耗。

并行处理技术

以三抽头的滤波器为例：$y(n)=b_0x(n)+b_1x(n-1)+b_2x(n-2)$
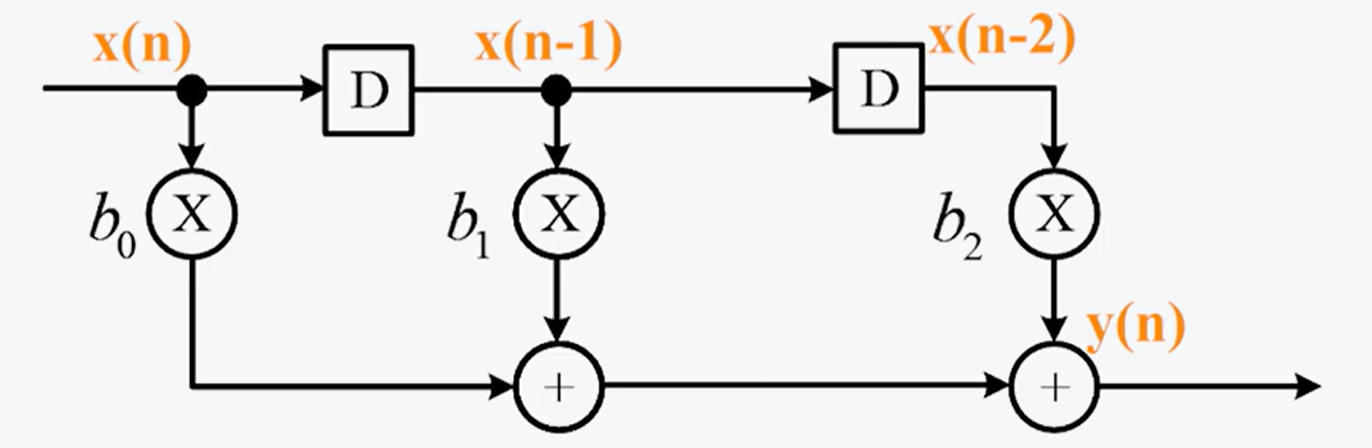
- 在下一个时钟周期计算$y(n+1)=b_0x(n+1)+b_1x(n)+b_2x(n-1)$
三抽头滤波器的两级并行：用$2k$代替上面两式中的$n$
$y(2k)=b_0x(2k)+b_1x(2k-1)+b_2x(2k-2)$ $y(2k+1)=b_0x(2k+1)+b_1x(2k)+b_2x(2k-1)$
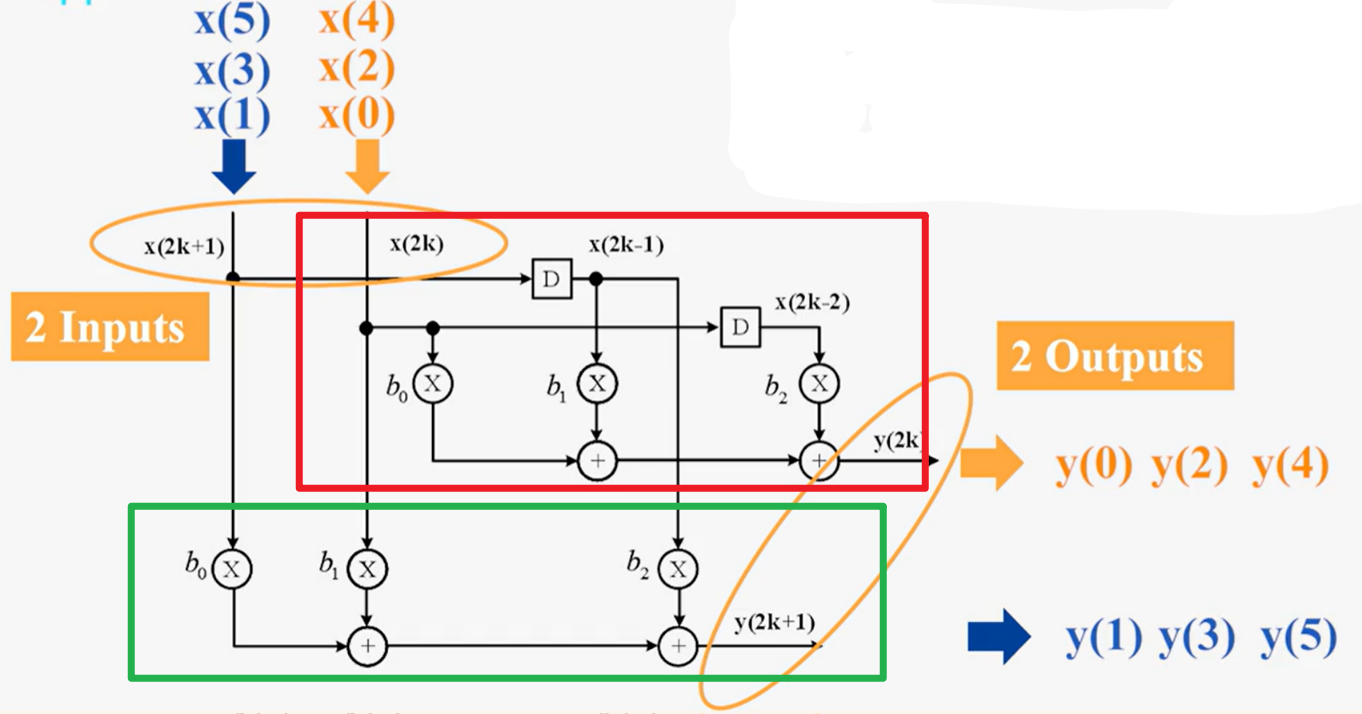
三抽头滤波器的三级并行：
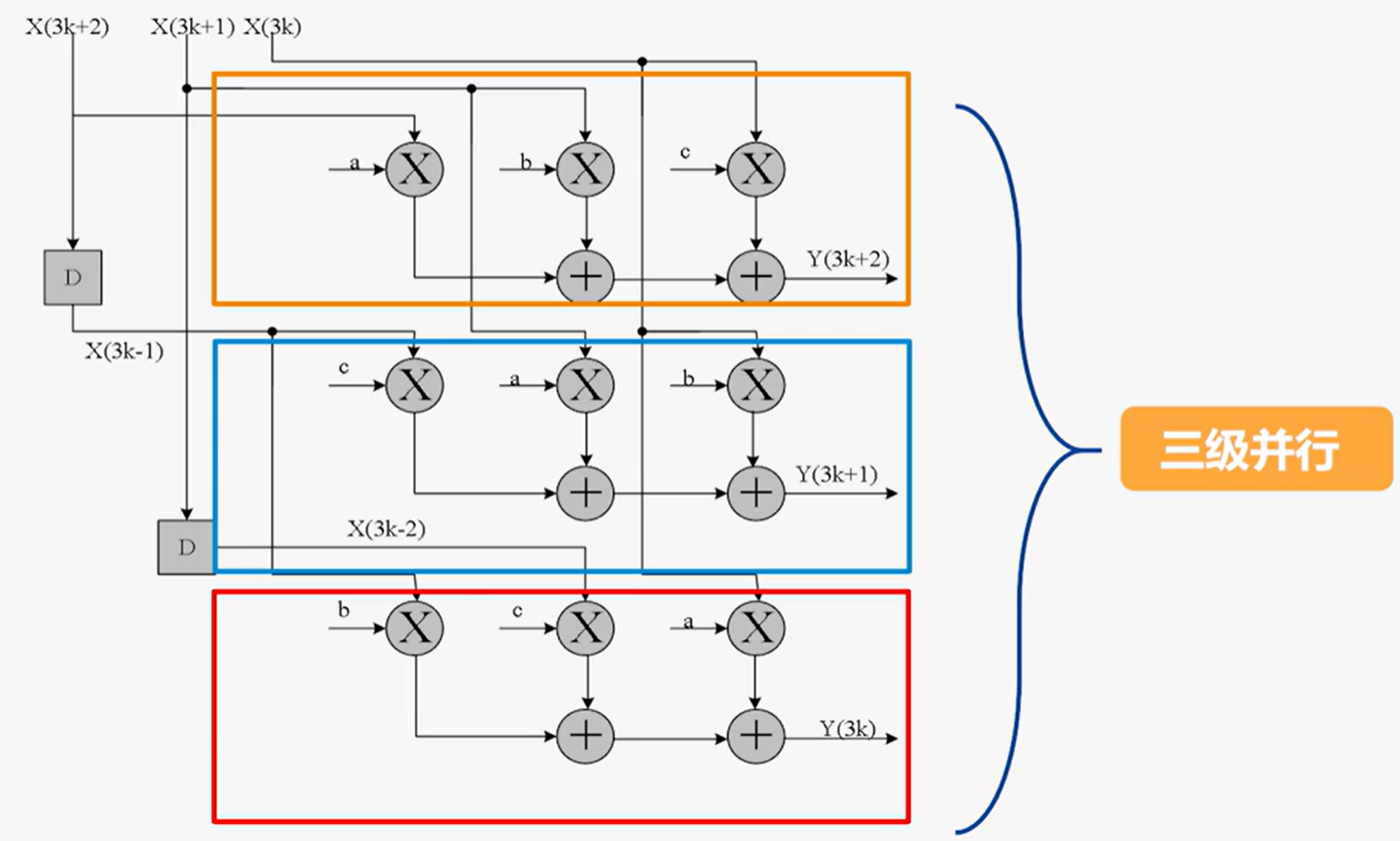
并行处理技术的特点：
- 并行处理系统的关键路径保持不变
- L级并行处理的一个时钟周期处理L个样点，则迭代（或采样）周期缩小为$\frac1L$
- L级并行系统的时钟周期：$T_{clk}=LT_{sample}$
- 时钟频率不变

流水线技术

技术关键：通过在数据通路中插入寄存器，减少关键路径长度，从而提高时钟频率
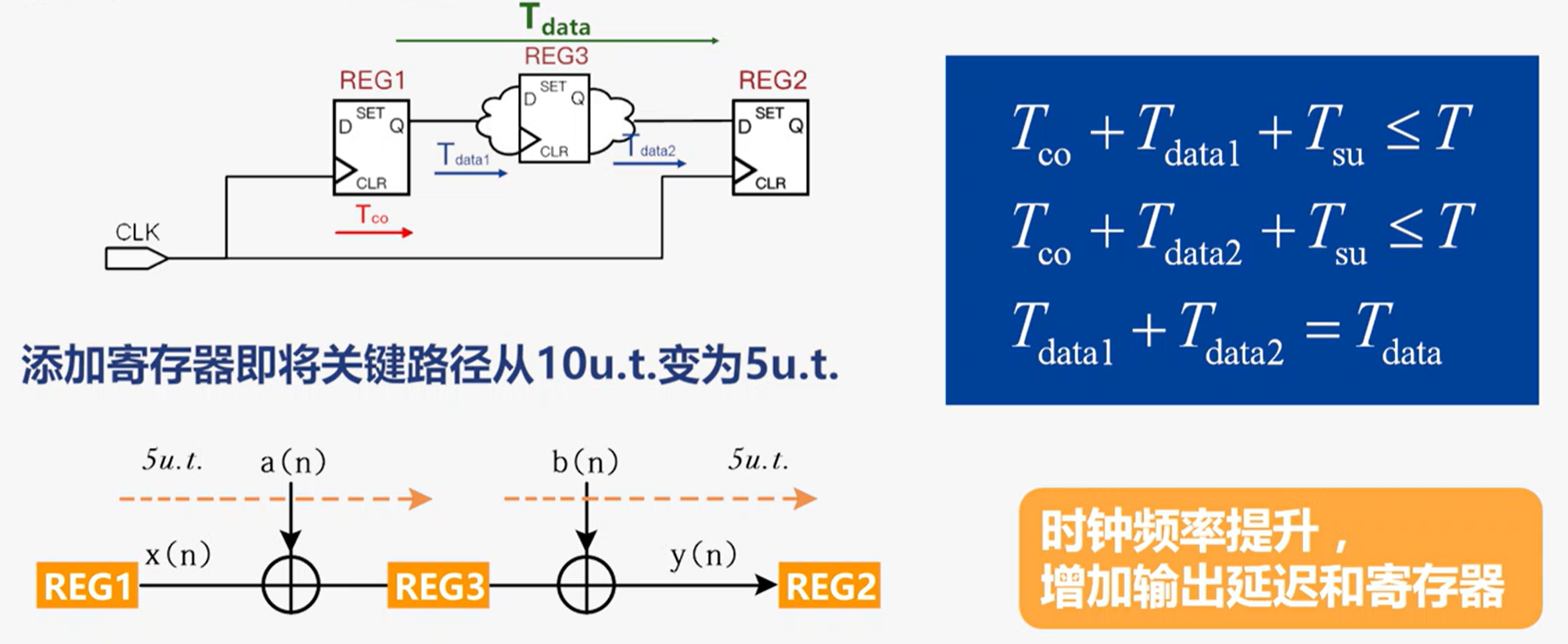
割集与前馈割集：
- 割集：是图的一组边，若从图中移走这些边，则图被拆分为互不相连的两个子图或孤立节点
- 前馈割集：数据沿割集所有同向移动，即割出来的边要么都是输入边要么都是输出边
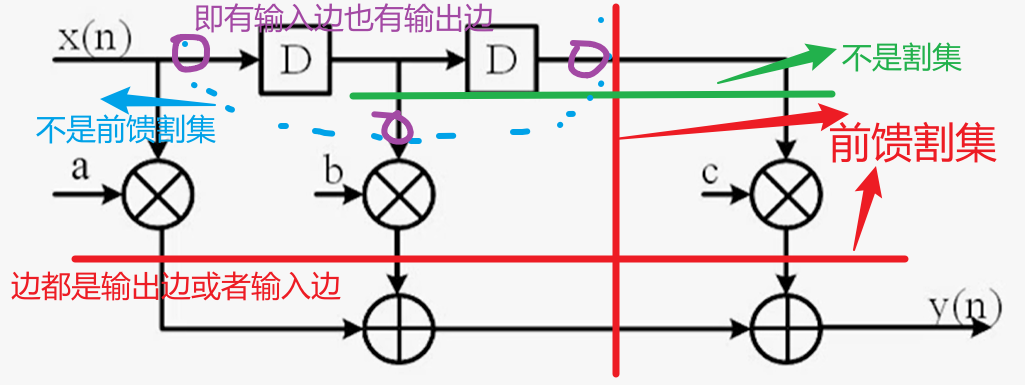
流水线技术是在前馈割集所有边插入寄存器，减少关键路径
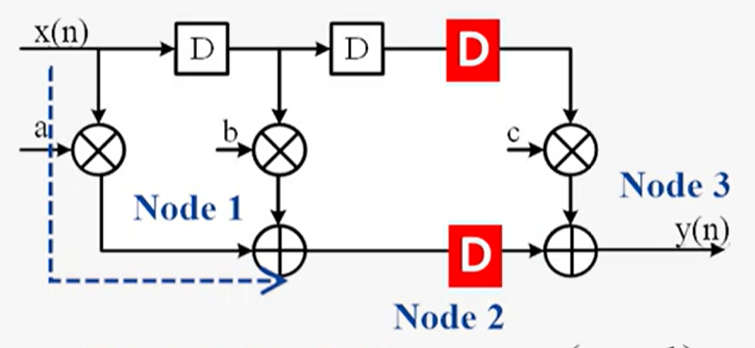
流水线的优缺点：
- 优点：缩短关键路径、提高时钟频率
- 缺点：增加寄存器的硬件开销，增加输出延迟
在M级流水线系统中，从输入到输出任一路径的延迟数比原系统中一路径的延迟数多$(M-1)$

流水线技术斩断了原始系统的有效关键路径，也相当于分解了原始系统的有效关键路径充电电容。约定以下符号：
$C_{o-charge}$：为旧电路关键路径上的等价充放电电容，上图的整段红线所代表的电容
$C_{n-charge}$：为新电路关键路径上的等价充放电电容，上图一小段蓝线所代表的电容
$V_0$：为旧电路工作电压
$\beta V_0$：为新电路工作电压，通过使得 $\beta$小于1降低工作电压的方法来降低功耗
$P_o$：为旧电路功耗
$P_n$：为新电路功耗
由于“理想”M级流水线的插入，使得$C_{n-charge}=\frac{C_{o-charge}}M$
传输延时公式中的充放电电容变小，而我们又不需要改变传输延时$T_{pd}$（$f=\frac1{max(T_{pd})}$）那么肯定能带来工作电压的减小，新旧电路传播延时相等
$T_{pd}=\frac{C_{o-charge}V_0}{k( V_0-V_t)^2}$ $T_{pd}'=\frac{\frac{C_{o-charge}}{M}\beta V_0}{k(\beta V_0-V_t)^2}$
有$T_{pd}=T_{pd}’$，则：
$\beta (V_0-V_t)^2=M(\beta V_0-V_t)^2$
通过上式可以求出$\beta$，进而改变工作电压从而降低电路功耗，此时的电路功耗为（总电容不变，时钟频率也不变）：
$P_n=C_{total}(\beta V_0)^2f=\beta^2C_{total}V_0^2f=\beta^2P_0$

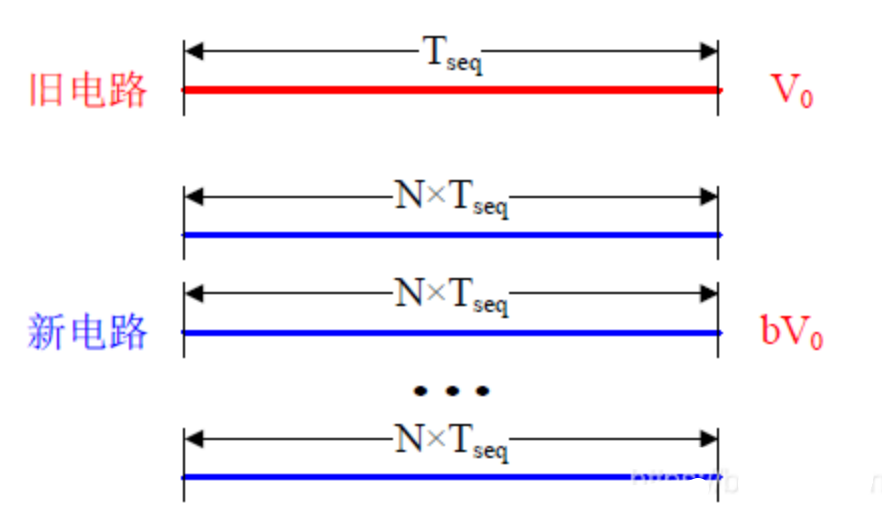
为保持原来的采样速率不变，L级并行处理系统的时钟周期增加为$LT_{seq}$，则电源电压可以降低到$\beta V_0$
$原时钟周期:T_{seq}=\frac{C_{charge}V_0}{k(V_0-V_t)^2}$ $新时钟周期:T_{seq}'=\frac{C_{charge}\beta V_0}{k(\beta V_0-V_t)^2}$
有：$T_{seq}’=NT_{seq}$，则：
$N(\beta V_0-V_t)^2=\beta(V_0-V_t)^2$
则新的电路功耗为（总电容变为原来的N倍，时钟频率变为原来的1/N）：
$P_n=NC_{total}(\beta V_0)^2\frac fN=C_{total}(\beta V_0)^2f=\beta^2P_0$
可以看到，$M$级流水线和$L$级并行处理的采用在不改变原始时序电路性能的情况下有相同的功耗降低能力